BTc “Binary Time constant” algorithm.
A system to record and/or play sound in a bitstream format using just one digital output pin.
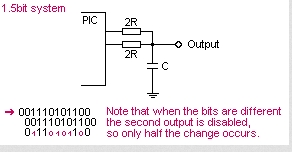
This is a sound playback system for a PIC or any other microcontroller. It uses a clever encoding system to mathematically model the actual performance of the RC filter when the signal is encoded. This allows playback of good quality sound with the absolute minimum software and hardware. The RC filter modeling (encoding algorithm) has been refined to be PIC friendly in binary math, giving the ability to playback AND RECORD in real time even on a PIC, even with high rates up to 150+ kbit/sec. The playback hardware is: 1 PIC digital output pin 1 resistor 1 capacitor
This makes it suitable for adding to small and low-cost products, providing speech or sound confirmation of keypress, talking PICs, sound record/playback devices, etc.
Playback theory:
With this system sound playback only requires an RC filter, and speaker, earphone socket etc. Sound playback is very simple and fast. Data is a single stream of bits, at a constant rate. The PIC only needs to output one bit, on one pin, at a regular timed rate to make the sound or speech. Sound can be added to an existing PIC project, if one pin and a few instructions each interrupt are available. Of course a digital output driving a simple RC filter is a common system, used in a number of cheap applications, but it has drawbacks due to the RC time constant giving a non-linear waveform. My BTc algorithm provides a simple fix, and is fast enough that it can do real-time compensation during encoding. The math modeling of my encoder maintains a model of the RC filter with zero accumulated error. If the bitrate is high enough this system will give CD-quality audio, due to the PWM effect of the dithering output, and the RC filter linearity problem is fully pre-compensated by the math modeling in the encoder. So the player doesn't need any math. :o)
Encoding theory:
Encoding the sound is the hard part. The stream of bits must be chosen correctly so that the final output waveform is as close as possible to the original waveform. But the actual output waveform depends on the electrical characteristics of the RC filter, ohms, uF etc. We can make the voltage on the RC filter rise by sending a "1" bit, or fall by sending a "0" bit, but unfortunately the voltage doesn't rise or fall by an equal amount for each bit... A form of compensation is needed to make the filter produce the correct waveform.
Encoding methods. In order to make the final playback waveform the closest reproduction of the original waveform I tried some closed-loop encoding systems, starting with the two most obvious types of encoding; REACTIVE: If sample is higher than math model make a 1 bit. If sample is lower than math model make a 0 bit. PREDICTIVE: In math model, make both bits, "predicting" each result. Then pick the bit that gives the output closest to the desired sound sample. Reactive is easier with only one model needing to be generated with each bit. Predictive works a lot better with all the sound samples I tried. I only used the predictive algorithm in my encoder program. Actually, I did support the reactive algorithm too, but deleted it later when it proved inferior. The trick is getting a fast and accurate math model generated, especially fast enough for high speed bitstream recording/encoding on a PIC.
BTc Encoding Algorithm:
I haven't seen this BTc algorithm used or claimed by anyone, it is basic encoding methodology, just done in a clever way to make it very easy and fast on a PIC. The use of "Binary Time constants" to make the filter calculation easy is my idea, but as always some other person may have thought of it before I did. I don't read enough technical papers these days. :o)
Why BTc??
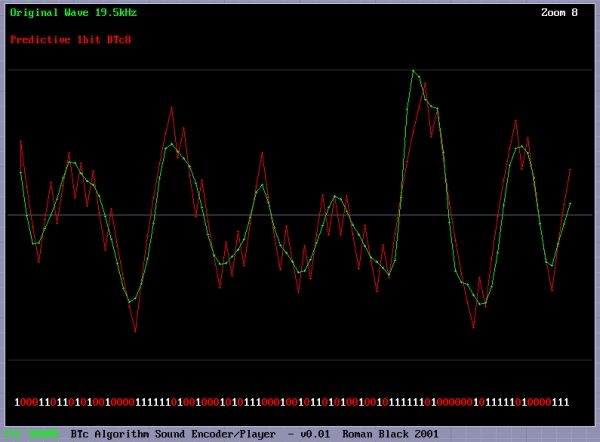
This was my solution to the problem of math modeling
the RC filter on a PIC, and allows high speed encoding.
To model the RC filter it requires using the "time
constant" or Tc=RC if you remember the math.
Tc=0.63208, and is not of much use to us when trying
to encode each bit in real time unless you have a
Pentium with floating point.
When I was testing different high speed encoding
solutions I came across a very simple idea. Instead of
calculating Tc as given and then doing more calcs to
reduce to a bit speed level suitable for encoding, I
could simply combine the whole lot if a specific Tc
could be assumed.
This allows ONE calculation, a simple binary division,
to do the entire RC math modelling!
If a SPECIFIC time constant is chosen, the TIME for
each bit matches the performance of the RC filter in
a very specific way, ie; the charge on C will rise by
exactly 1/4 or 1/8 or 1/16 during the time that it
takes for one bit! Magic.
Here are the binary time constants, which I have
provided for you;
BTc2 = 0.6931 x Tc (voltage changes 1/2 each step)
BTc4 = 0.2877 x Tc (voltage changes 1/4 each step)
BTc8 = 0.1393 x Tc (changes 1/8th etc)
BTc16 = 0.0645 x Tc
BTc32 = 0.0317 x Tc
BTc64 = 0.0157 x Tc
Real world example?
So if we choose the BTc8 system, we know that the
charge (voltage) on the C of our RC filter rises
or falls by 1/8th of the remaining voltage with every
bit in our playback bitstream.
To do this we just need to tune the RC filter values
to our required bitrate. Don't worry too much about
the math, at the bottom of this page I have provided
software that will display your sound wave, encode it
in the way you choose, and display the encoded "math
model" waveform so you can see the actual waveform
you will get on your RC filter. Then it will save the
bitstream as a data file or even as complete PIC code
with the sound data as RETLW table, ready to program
directly into a PIC chip and play the sound back.
The math stuff
Imagine a PIC with 16MHz crystal, giving 4,000,000
instructions/sec. Now using prescaler=0 the timer0
interrupt occurs at 15625 Hz. That is an ideal rate
for our sound playback on a PIC.
Bitrate: 15625 Hz
(We choose BTc8) = 0.1393
So BTc8 = 0.1393 @ 15625 Hz
Therefore Tc = 0.1393 x 15625
Tc = 2177 Hz
Tc = 1 / 2177 = 0.000459 seconds
Tc = RC
R = Tc / C
(let's assume 0.1uF for convenience)
R = 0.000459 / 0.0000001
R = 4595 ohms
Hope that doesn't look too scary, but what we have
done is found that for our desired bitrate at
15625Hz, we can use an RC filter of 4595 ohms and
0.1uF capacitor, and for every bit which occurs
at 15625Hz the voltage on our RC filter will rise
or fall by EXACTLY 1/8th.
Now we can encode in real time on a PIC, and the
main filter math is a couple of add/subtracts and
one divide by 8.
This means we only have to do a handful of very simple
calculations for each bit. We can do the entire
encoding process and produce the encoded bitstream in
real time on a PIC to be played back perfectly on any
other PIC with just a resistor and capacitor. How cool.
Below is an example showing the BTc8 algorithm
encoding a file which contains speech and background
music. This is the BTc8 1bit algorithm on a 19.5kHz
sound. 19.5kHz = 20MHz PIC interrupted every 256
instructions. The RED wave is the encoded waveform,
as you can see it is a decent reproduction of the
original sound waveform (green). The "spiky" points
of the wave are not really important as they will be
filtered by the speaker inductance, or a simple
post-filter if needed. The main thing is that the
AVERAGE of the wave is a decent reproduction of the
original, as that is how your ear will hear it. :o)
You can still see the non-linearity in the encoded
waveform, look anywhere there are a few 1s or 0s
in a sequence. However this does not matter as the
encoding process allows for all errors and still
produces an acceptable reproduction waveform.
For more detail: Record+play fast 1bit sound on a PIC!
