Introduction
For this design project, we built a portable digital synthesizer capable of creating a wide variety of sounds designed by the user. The system consisted of a full octave (13 key) keyboard with two-voice polyphony, three rotary encoders for user input, a TFT LCD for visual display, and an SPI DAC for audio output. A user can play up to 2 notes simultaneously, and adjust many parameters of the system’s digital sound synthesis on the fly. Wave lookup tables were used to produce different waveforms, including sine, square, sawtooth, and noise waves. Frequency and amplitude modulation were used to create more complex waveforms. For easy portability, the entire system was contained within a 18.8 cm x 10.6 cm x 2.3 cm 3D-printed enclosure. The entire project is based on the PIC32MX250F128B microcontroller.
High Level Design
An important design consideration of our digital synthesizer was portability. Many synthesizers are large and bulky, with huge keyboards. We wanted ours to be much smaller, with a focus on sound design, rather than use in performances. We felt that increasing portability, while still developing a system that could produce a wide range of sounds, was an effective way to distinguish our design from those of other digital synthesizers. With this goal of portability in mind, we wanted to keep the internal hardware of the system as compact as possible. Additionally, we wanted to create a custom enclosure to protect the electronics and make the system easier to move around. Making the system easy to start up was another goal. We aimed, and were able, to make a system which only required the user to plug in a power supply and speakers/headphones in order to start up.
Another important design consideration was the user interface. Despite making the system relatively small, we still wanted the user interface to be easy-to-use. On the input side, we chose to arrange 13 push buttons in a keyboard configuration. Using 13 buttons allowed us to fit a full octave’s-worth of keys in a configuration close to what is found on a piano or keyboard. We initially considered using keypads for the keys, but we felt that using push buttons would allow us to space the keys better and make the system easier to play. To enable parameter changing, we decided to use three, prominent rotary encoders whose positions could be mapped to different system parameter values. We considered using potentiometers for the same purpose, but using rotary encoders eliminated the need for ADC channels. We were also able to find rotary encoders with built-in push buttons, which we were able to take advantage of. On the output side, we opted to use the TFT LCD to convey system information to the user. We chose to organize the display into a series of screens, and each screen showed three different system parameters whose values could be changed using the rotary encoders. We also decided to use the push buttons on the rotary encoders to transition between different system screens. We felt that organizing the display in this manner would clearly convey the current system state to the user.
We also wanted to optimize the execution time, and allow flexibility in the code to add new user-adjustable parameters. Much of the software design focused on making the code execute as quickly as possible, so the synthesizer would respond immediately to user input, have high quality sound output, and show no flickering on the TFT screen. This is outlined in the Software Design section.
As with all design projects of this kind, tradeoffs were necessary. We encountered one such tradeoff when deciding how many push buttons to add. The more push buttons we added, the less compact the system would have been. Adding two-octave’s-worth of keys may have enhanced the user experience, but it would have made the system almost 100% bigger and put us in jeopardy of running out of I/O pins to use. We had to consider another tradeoff when choosing the sample rate for sound synthesis. The higher the audio sample rate, the greater the CPU load. We ended up settling on a sample rate of 20 kHz. Choosing a standard sample rate like 44.1 kHz would have increased the quality of the sound produced, but it also would have more than doubled the CPU load when performing the synthesis. Additionally, at a sample rate of 20 kHz, we could generate frequencies up to 10kHz, which is much of the useful range of human hearing. As you can see, when considering tradeoffs, it was important to weigh the different options in order to determine which decision was most appropriate for our project.
These references provide more background information on the processes we used for sound synthesis.
Hardware Design
There were several noteworthy hardware elements of our design. First, we needed the push buttons which the user would press to produce different tones. We needed the rotary encoders to enable the user to adjust the system parameters. In order to handle all the inputs to the synthesizer, it was necessary to add a port expander. We used an SPI DAC to output the audio signals to an audio socket, into which the user could plug a pair of speakers or headphones. A TFT LCD was used as the visual output device. Finally, the entire system was housed within a 3D-printed enclosure. We will now discuss all of these elements in greater depth.
Push Button Matrix:
As stated before, we used push buttons for the keyboard on our digital synthesizer. There were 16 total push buttons in our design: 13 4-pin push buttons (description here) and 3 built-in push buttons on the rotary encoders. In order to reduce the number of I/O pins needed to use these push buttons, we decided to connect them in a 4×4 matrix configuration. Figure 1 shows a schematic of the button matrix. A different push button was placed at each of the intersections between the rows and columns. Using this configuration allowed us to detect presses on 16 push buttons using only eight I/O pins. The rows on the figure connect to output pins on the port expander (labeled Y0-Y3), and the columns connect to input pins on the port expander (labeled Y4-Y7). We have labeled the intersections between the rows and columns with numbers, and these numbers identify the position of the corresponding push button, according to Figure 2.
In order to detect presses, we used a relatively straightforward procedure. First, note that the internal pullup resistors connected to the input pins indicate that this system was active low. The output pins sequentially sent low pulses onto the rows, one row at a time. The input pins monitored the voltage of the column they were connected to and registered a button press whenever they detected a low-voltage signal. In order to tell which button was pressed, we simply needed to know which output pin was sending the low pulse (only one output could be low at a time) when the low-voltage signal was detected by one of the inputs. The button at the intersection of the row onto which the low pulse was being sent and the column on which the low-voltage signal was detected must, therefore, have been the button that was pressed. For example, if a low-voltage signal was detected by Y5 when a low pulse was being sent on Y0, then the system knew that button 2 was pressed.
The diode on each row of the matrix was needed to prevent missed presses when two buttons in the same column were pressed simulataneously. We will discuss these diodes further in the Testing section.
Rotary Encoders:
The rotary encoders we used were from Bourns’ PEC11 series (datasheet here). These encoders had five pins: three for the actual rotary encoder and two for the built-in push button. As we mentioned in the High Level Design section, the rotary encoders were used to adjust system parameters, and the built-in push buttons were used to transition between different screens on the display. These rotary encoders had 24 angular positions equally spaced across 360 degrees of rotation. We will now discuss how to decode the output from such encoders.
Figure 3: Rotary Encoder Outputs
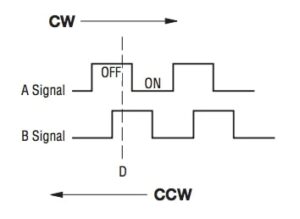
Like we stated above, the actual rotary encoders had three pins. Two of these were signal pins, and the third was a common (ground) pin. The image above shows the output on the two signal pins for clockwise and counterclockwise rotation when the pins are connected to internal pullup resistors on a microcontroller. Our system read these two signals for each rotary encoder using two pins on the port expander (six pins total). Connecting the signal pins on the rotary encoders to pullup resistors meant that they would be at logic high when they were idle. During the transition between angular positions, each signal pin would come into contact with the common pin. This would cause the pins to discharge and fall to logic low. The key to the device is that the signal pins do not come into contact with the common pin at exactly the same time. If the device is rotated clockwise, the A signal pin comes into and out of contact with the common pin before the B signal pin. If the device is rotated counterclockwise, the B signal pin comes into and out of contact with the common pin first. As you can see from the image, the two signals are 90 degrees out of phase.
We then were able to detect and distinguish clockwise and counterclockwise rotations using the following logic: When a logic high to logic low transition is detected on the A signal, the system checks the current state of the B signal. If the B signal is logic high, then the rotation must be clockwise. If the B signal is logic low, then the rotation must be counterclockwise. Once these rotations were detected, they could be used to increase or decrease the values of different system parameters. In the Software Design section, we will discuss how we implemented debouncing to prevent sporadic behavior when trying to detect rotations.
Port Expander:
In order to avoid running out of I/O pins on the PIC32, we chose to use the MCP23S17 port expander (datasheet here). The port expander used SPI to communicate with the PIC32 microcontroller we integrated into our design. The expander gave us 16 extra I/O pins to use (Y0-Y7, Z0-Z7). As briefly stated in the Push Button Matrix section, we used pins Y0-Y7 as the input and output pins for the matrix. We also used pins Z0-Z5 as the six pins connected to the signal pins of the rotary encoders.
SPI DAC:
To enable audio output, we used the MCP4822 SPI DAC (datasheet here). As we will discuss in the Software Design section, we used wave lookup tables, frequency modulation, and amplitude modulation to produce digital audio signals. These generated signals were then sent to the DAC via SPI, where they were converted into analog signals capable of being played on a set of speakers or headphones. The DAC had two output pins, A and B. We chose to connect DAC output pin A to our audio socket input.
Audio Socket:
Figure 4: Audio Socket

To audibly play our audio signals, we connected our DAC output to a set of lab speakers via an audio socket. We also could have connected headphones to the audio socket. The audio socket we used is shown above. The pin closest to the socket is the ground pin. The other two pins are both signal input pins, and we chose to connect one of these pins to the DAC output. After the audio socket was connected, we could simply plug the speaker or headphone jack into the audio socket, in order to hear the synthesized sounds.
TFT LCD:
As we mentioned earlier, a TFT LCD was used as the visual output device for our project. More documentation for the TFT we used can be found here. The TFT had 320×240 color pixels and communicated with the PIC32 via SPI.
Enclosure:
We wanted to make a custom enclosure for our synthesizer, in order to make the design as compact as possible and to protect the internal electronics. We decided that 3D-printing an enclosure would most likely be the easiest way to make a design that was exactly the dimensions we wanted. Once the internal electronics were fully assembled, we made some careful measurements and designed our enclosure using Autodesk Tinkercad. We had to design and print the enclosure in three pieces: one piece for the base and two pieces for the top. We took the STL files we made in Tinkercad and used Ultimaker Cura to convert them to G-Code files. We then used a Monoprice Maker Select V2 3D printer to actually print the G-Code files. Once the three pieces were printed, we reinforced any weak spots with hot glue and assembled them around the electronics.
Figure 5: Design for Enclosure Base

The image above shows the base of the enclosure in Tinkercad. The maximum dimensions of the enclosure were 18.8 cm x 10.6 cm x 2.3 cm. However, the dimensions varied for different sections. The height was only 1.5 cm around the push buttons and rotary encoders, while it was 2.3 cm around the TFT. We were also able to decrease the amount of material we needed to print by eliminating the section in the top right (when viewed from above).
Software Design
The main focus of the software design was to optimize the execution time, and allow flexibility in the code to add new user-adjustable parameters. To optimize execution, we used phase accumulators and fixed point arithmetic for DSP and fast debouncing algorithms. We also moved slow calculations with floating point numbers and divisions to the slower input threads, which only needed to be updated on a millisecond scale within human reaction time. Finally, we updated the TFT LCD screen only when necessary. To allow flexibility in the code, we created a Param structure to contain all information for adjustable parameters. Thus, when we wanted to add a new parameter, we just created a new Param structure.
Structures:
We used two structures to organize our data: a Note structure and a Param structure. Notes refer to the keys that a user can press, and Params refer to the various parameters of the DDS algorithm that the user can change.
Note: Each Note has 6 values, which store information for the DDS algorithm. Thirteen Note structures are stored in noteArray — one for each key on the keyboard.
int pressed: If the note is currently pressed,pressed = 1. Otherwisepressed = 0.int active: does sound need to be generated for that note?int main_stateandint fm_state: the current ADSR state for the main/fm waveformint phase_incr_mainandint phase_incr_fm: determines the phase increment for the main/fm waveforms.
Param: Each Param also has 6 values, which contain information for the DDS algorithm, as well as how the user can change the parameters. There are 15 Params available, which are stored in the array paramArray.
int no: each Param has its own number, which designates its position inparamArray.int flag: if the value of the Param has changed,flag = 1._Accum maxand_Accum min: the maximum and minimum values that the Param can take._Accum val: the current value of the Param._Accum inc: the amount the Param increments or decrements on each turn of the rotary encoder.
The following 15 Params can be changed by the user:
- Output Volume: changes the amplitude of the final output waveform.
- Octave: changes the Note frequencies.
- Preset: cycles through preset sounds (this feature has not yet been implemented).
- Main Waveform: cycles through waveforms for the main wave (sine, square, sawtooth, noise).
- FM Waveform: cycles through waveforms for the FM wave (sine, square, sawtooth, noise).
- FM Volume: changes the amplitude of the FM wave (also known as FM depth).
- FM Ratio: changes the ratio of the FM frequency to the main frequency.
- Main Attack: the rate at which the main wave ramps up from 0 to full volume.
- Main Decay: the rate at which main wave ramps down from full volume to sustain volume.
- Main Sustain: the sustain volume of the main wave.
- Main Release: the rate at which the main wave ramps down from sustain volume to 0.
- FM Attack: the rate at which the FM wave ramps up from 0 to full volume.
- FM Decay: the rate at which FM wave ramps down from full volume to sustain volume.
- FM Sustain: the sustain volume of the FM wave.
- FM Release: the rate at which the FM wave ramps down from sustain volume to 0.
Figure 6: Block Diagram

Fast Direct Digital Synthesis in ISR:
The most important part of our synthesizer is the fast DDS algorithm that is run in the ISR. The ISR is triggered by Timer2 to run every 2000 cycles, which results in a 20 kHz sampling rate. (20 kHz samples per second = 40 MHz cycles per second / 2000 cycles per sample). It reads all of the current values of the various parameters and performs quick fixed point arithmetic to calculate the next sample to output to the DAC over SPI.
For FM synthesis, two waves need to be generated: the main wave, and the FM wave which modulates the frequency of the main wave. Various waveforms (sine, square, sawtooth, and noise) are stored in 256 element lookup wave tables, with values ranging from -1023 to 1023. This range is to ensure 2 notes can be played simultaneously over the 12-bit DAC. To choose the correct value in the wave table we use 32-bit phase accumulators and phase increments for both the main and FM waves. To generate a fixed-frequency wave, the constant phase increment is added to the phase accumulator every ISR call. A large phase increment steps quickly through the wave lookup table, generating a high frequency wave, and a small phase increment creates a low frequency wave.
First, we generate the FM wave. To create the FM wave at frequency Fout, we set phase_incr_fm = (Fout * 232) / Fsampling. We multiply by 232 to scale the increment value to 32 bits. Every ISR call, the phase increment is added to the phase accumulator, which is shifted to the right by 24 bits to index into the wave table. The main wave is generated similarly, but the value of the FM wave shifted left by 19 bits is added to the phase increment of the main wave. This is how the FM wave modulates the frequency of the main wave.
The use of phase accumulators/increments makes our sound generation very efficient. All the phase increments are calculated in a seperate thread, since they involve slow float division. Thus, the ISR only needs to do a quick integer addition, bit shift, and lookup to an array. Due to the many user-adjustable parameters, the ISR also performs a number of multiplications to determine the output volume, FM volume, and ADSR envelopes. These value of these Params range from 0 to 1, and are fixed point _Accum variables with 16 integer bits and 15 fraction bits. Fixed point multiplication was used to decrease the execution time. Multiplication with _Accum variables take 28 cycles, compared to 55 cycles for float multiplication.
Similarly to the phase increments, we calculate the ADSR envelopes using envelope increments to improve execution time. Outside the ISR (see the input thread), increment values are calculated for the attack, decay and release. Thus, inside the ISR, we only need to add or subtract these increments from the current envelope value, based on the current state of each note. Each note has its own state for both the main waveform and FM waveform: 0=inactive, 1=attack, 2=decay, 3=sustain, 4=release. The ISR runs a state machine for all the active notes, and transitions between states based on the current value of the envelope and user input. Thus, we can generate the main and FM envelopes completely independently.
Compact Rotary Encoder Debouncing in ISR:
We also read the rotary encoder pins in the ISR, because reading at a millisecond scale was too slow to capture every turn of the encoder. The rotary encoders are connected to the port expander, so we read the bits over SPI using the readBits function provided in port_expander_blr4.c. However, rotary encoders are very noisy, so we need to debounce the readings. We use the following digital debounce filter:
state0 = (state0<<1) | A0_input | 0xe000;
Each time the ISR is called, the reading of the A terminal of the rotary encoder (A0_input) is shifted left into the integer state0. The 0xe000 is included to block the top 3 bits, since we only care about the first 13 bits. To determine if the encoder has transitioned from high to low, we check for state0 == -4096, which is equivalent to state0 == 0xf000. This means that state consists of a 1 followed by twelve 0’s, so we know the signal has been stable. Finally, if this check passes, we can tell which direction the encoder was turned based on the B terminal. If the B terminal is high, the turn was clockwise. Otherwise, the turn was counter-clockwise. The code for this filter was provided by best-microcontroller-projects.com.
Finally, parameters values are updated based on the rotary encoder readings. We keep an array of the 3 parameters that are currently active called activeParams. The value of the parameter Param.val is incremented by Param.inc if the associated encoder was rotated clockwise, and decremented by -Param.inc if it was rotated counter-clockwise. Also Param.flag is set to 1, so other threads know the parameter has been changed.
Input Thread:
Next is the input thread, which is run every 20 ms. This thread reads the push buttons so the correct notes are played, and also performs the slower calculations. This thread contains code that doesn’t need to be run as quickly as the ISR, but just needs to be faster than the average human reaction time of ~200 ms. Also, debouncing is not necessary, since the buttons are read at a slow rate.
The push buttons are connected to the port expander, which is accessed through SPI. Since the DAC data is also output through SPI, we need to create a critical section whenever we access the port expander. The critical section is enabled by turning the interrupt off for Timer2. To read all the push buttons on the keypad matrix, we need to set each horizontal line on the keypad low, and then read the vertical lines. See Hardware Design for more information. To do this, we used the writePE and readBits functions provided in port_expander_blr4.c. The readings are then decoded and stored in the 16-element array keys, where keys[i] contains the pressed state of the ith note (1 if pressed, 0 otherwise). Here we also update all the pressed values of the Note structures, so the ISR knows what notes are currently being pressed.
Next, we calculate any slow calculations that involve float multiplications or _Accum divisions. This includes recalculating phase increments if the Octave or FM Ratio Params change, or ADSR envelope increments if the ADSR Params change. To improve performance, we only perform these calculations if the associated Params have flags that have been activated.
Lastly, we check the push buttons connected to the rotary encoders. If a single rotary encoder is pressed, this changes which parameter is active on that encoder, so we update the activeParams array. We also set the param_name_flag to 1, so the frame thread knows it needs to update the parameter name and value. To prevent many parameter transitions from occuring on a single button push, we only change parameters on a low to high transition of the button. Additionally, if the left or right rotary encoder transitions from low to high while the middle encoder is held down, we change screens, and set the screen_flag to 1. Each screen has its own set of parameters that can be changed. More information is in the description of the Frame thread. To prevent the middle parameter from being adjusted while changing screens we have a button_flag, which ignores the release of the middle button after changing screens.
Optimizing the Update Frame Thread:
The screen is updated at 10 frames per second, or once every 100 ms. Drawing to the TFT takes many cycles, so we optimize by drawing only what is necessary. Each parameter on the screen has a title, value, and bar to visualize the range of possible values. We created the helper functions drawTitle, drawValue, and drawBar to draw these elements at different positions on the screen. If param_name_flag is active, there’s an entirely new active parameter, so we redraw the parameter name, value, and bar. If Param.flag is active for a particular parameter, we redraw the value and bar. If screen_flag is active we need to update the screen heading, as well as the title, value, bar and color of each parameter.
The following pictures demonstrate the various screens:
Figure 7: System Screens

Main Settings include Params 0 to 2, Waveform Designer includes Params 3 to 6, Main Envelope includes Params 7 to 10, and FM Envelope includes Params 11 to 14.
The parameters were split up in this fashion, so a user could easly find the parameter they wanted to change, rather than cycling through all 15 parameters.
Testing
During the design of our system, we performed many tests to determine the speed of execution time. To ensure the system was responsive, we checked the number of cycles it took to perform the ISR, and the number of milliseconds to execute the Input and Update Frame threads. Through multiple tests, we were able to reduce the ISR execution time from a maximum of 1800 cycles to 1200 cycles. The ISR time was shortened by using _Accums for multiplication and using a fast debouncing algorithm for the rotary encoders. Also, storing the phase accumulators and envelopes in a global array, rather than as a parameter in each Note structure, greatly improved execution time. Additionally, by only updating the TFT when necessary, we were able to reduce the Update Frame execution time from 100ms, down to 7 ms, when no parameters were changing. More information on the execution time can be found in the results section.
We originally did not include the diodes on the rows of our push button matrix, as seen in Figure 1. When we were testing the functionality of our push button matrix, we discovered that pressing two buttons in the same column resulted in no presses being registered. The issue was that pressing two buttons in the same column simultaneously connected a row at logical high and a row with the low pulse to one column at the same time. This caused the column to take a logical value somewhere between logical high and logical low. This prevented the low pulse from being detected by the input pin connected to the column. Adding a diode to each row fixed this issue because the diodes prevented output pins at logical high from recharging a column with the low pulse on it. The diodes had to be oriented such that they only allowed current flow towards the output pins, not from the output pins. This allowed the columns, which were at logical high when idle, to discharge through an output pin when that output pin sent a low pulse. This effectively transmitted the low pulse signal to the input pins connected to the columns. At the same time, the directional nature of the diodes isolated a column with a low pulse signal on it from the logical high signals on the other output pins.
One unresolved issue with our push button matrix is what is known as the ghosting problem. The ghosting problem occurs when three buttons in the same rectangle (as seen in Figure 1) are pushed simultaneously. This causes the fourth button in the rectangle, which is not actually pressed, to appear to the microcontroller as though it is pressed. One way to resolve this issue is to slightly modify the push button matrix by moving the push buttons just above the intersections on the columns and adding diodes that connect each push button to the correct row. If we were to do the project over again, we would try to implement this scheme for the push button matrix because we would then reliably be able to press several buttons at the same time.
Results
The video of our project demonstration can be found here. As you can see, the entire system fits within a relatively small enclosure. You can get a better idea of the look of the display screen and the responsiveness of the system to user input. You can also get a small sample of the different sounds the system is capable of producing.
As we stated earlier, we used wave lookup tables to produce four different kinds of waveforms: sine waves, square waves, sawtooth waves, and noise. The following are oscilloscope screen captures of the waves we produced:
Figure 8: Sine Wave

Figure 9: Square Wave
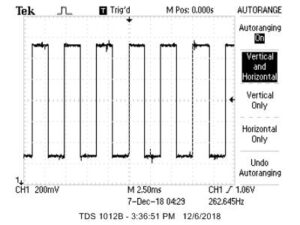
Figure 10: Sawtooth Wave
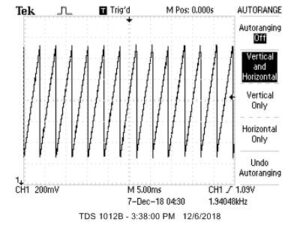
Figure 11: Noise

We used the Fast Fourier Transform (FFT) on the oscilloscope to confirm the frequency content of our outputs. Below, we show screen captures of two FFTs. The first shows the FFT of an A-440 sine wave. Using the horizontal scale of 125 Hz per box, we can see that the fundamental frequency is almost exactly at 440 Hz, like it is supposed to be. The second shows the FFT when the high and low C of an octave are played together. We can see that the second fundamental peak is at almost exactly twice the frequency of the first fundamental peak, like we would expect.
Figure 12: A-440 FFT

Figure 13: High and Low C FFT

We were able to gather the following frequency accuracy data for sine waves generated by our system:
Figure 14: Frequency Accuracy Data
| Note | Measured Frequency | Target Frequency | Absolute Difference | Percent Error |
|---|---|---|---|---|
| Low C | 262.8 | 261.6 | 1.2 | 0.459 |
| C-sharp | 278.0 | 277.2 | 0.8 | 0.289 |
| D | 295.1 | 293.7 | 1.4 | 0.477 |
| E-flat | 313.5 | 311.1 | 2.4 | 0.771 |
| E | 330.0 | 329.6 | 0.4 | 0.121 |
| F | 351.5 | 349.2 | 2.3 | 0.659 |
| F-sharp | 372.0 | 370.0 | 2.0 | 0.541 |
| G | 393.8 | 392.0 | 1.8 | 0.459 |
| G-sharp | 418.0 | 415.3 | 2.7 | 0.650 |
| A | 440.8 | 440.0 | 0.8 | 0.182 |
| B-flat | 467.2 | 466.2 | 1.0 | 0.215 |
| B | 496.0 | 493.9 | 2.1 | 0.425 |
| High C | 522.0 | 523.3 | 1.3 | 0.248 |
This gave us an average percent error of 0.423% between the target frequencies and the actual frequencies produced by our synthesizer. We are very pleased with this level of accuracy.
To get an idea about our maximum CPU load, we calculated the number of cycles the system took to execute the sound generation ISR and saved this number in a variable. This ISR was configured to run at 20 kHz, meaning that its execution was triggered by a timer interrupt every 2000 cycles. We printed the variable on the TFT to see its value. When the system was idle (no buttons pressed), it took 783 cycles to execute the ISR. When one note was played, it took 1015 cycles to execute. When two notes were played, it took 1200 cycles to execute. Dividing 1200 by 2000, the number of cycles between executions of the ISR, tells us that our maximum CPU load is roughly 60%.
Our goal was to maintain a frame rate of at least 10 Frames/second. This means that we wanted the system to take no longer than 100 ms to redraw the screen. We were able to gather the following frame rate data:
Figure 15: Frame Rate Data
| Condition | Time to Draw Screen (ms) | Frame Rate (FPS) |
|---|---|---|
| No Notes Played | 7 | 142.9 |
| 1 Note Played | 9 | 111.1 |
| 2 Notes Played | 11 | 90.9 |
| No Notes w/ Screen Change | 125 | 8.0 |
| No Notes w/ Param Change | 60 | 16.7 |
| 1 Note w/ Screen Change | 155 | 6.5 |
| 1 Note w/ Param Change | 77 | 13.0 |
| 2 Notes w/ Screen Change | 170 | 5.9 |
| 2 Notes w/ Param Change | 82 | 12.2 |
As you can see, we were able to maintain at least a 10 FPS frame rate for every condition, except when the system changed between screens. However, these screen changes happened so quickly that the frame rate lag was almost unnoticeable to the user.
Conclusions
Expectations & Future Work:
We were able to meet many of our goals. The synthesizer was able to create a wide variety of high-quality, user-generated sounds, and was immediately responsive to user input. It was also easily portable, with a simple user interface.
In the future, there are many features we could add to improve the functionality of the design. On the hardware size, we could add the diodes as described in the Testing section, to allow the user to press more than 2 keys simultaneously. This would allow the user to play many different chords. Also, we could move the rotary encoders directly to the PIC32 microcontroller, rather than the port expander. This would greatly improve our ISR speed, since we found that it took 200 cycles in the ISR just to read the port expander. We could further improve execution speed by generating interrupts when the rotary encoder terminals change, rather than polling the ports continuously.
On the software side, there are many features that could be added. The most useful would be saving sound presets. This way the user can create a sound, and then save it to play again later. Another fun feature would be a looping feature, which could allow the user to create a full song.
Intellectual Property Considerations:
There are no intellectual property concerns for our sound synthesis algorithm. Phase accumulators, frequency modulation, and ADSR envelopes are all commonly used techniques for generating sounds. We used Professor Bruce Land’s FM synthesis code as reference for our algorithm.
We also used a compact filter to debounce our rotary encoders provided by best-microcontroller-projects.com.
We don’t believe there are patent opportunities for our project.
Safety Considerations:
Our system is very safe. There are no stray wires since all of the electronics are enclosed by a 3D printed box. Also, there are no high power electronics or moving parts.
