Introduction
The Julia Set, was used to generate fractal art on the TFT. The Julia Set can be described by 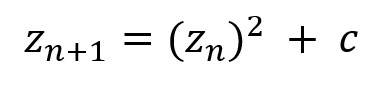 , where z represents a point on the complex plane and c is a complex constant. In order to allow for user manipulation and interaction, a GUI was implemented. The GUI allows for users to first select a color scheme (red, yellow, green, turquoise, blue, purple, or rainbow). From there, they can either input the real and imaginary parts of a complex constant or select a designated preset to generate a design. Once the design is drawn, the user can used a keypad to zoom in on one of the quadrants. Once zoomed in, the user can zoom out using the keypad as well. To clear, the user can either select a button on the keypad or the GUI. By implementing the design this way, we were able to incrementally increase complexity and allow for more complex interaction with the design. Also, the project allowed for manipulation and constant discovery of new designs and coloring with each set of selected parameters.
, where z represents a point on the complex plane and c is a complex constant. In order to allow for user manipulation and interaction, a GUI was implemented. The GUI allows for users to first select a color scheme (red, yellow, green, turquoise, blue, purple, or rainbow). From there, they can either input the real and imaginary parts of a complex constant or select a designated preset to generate a design. Once the design is drawn, the user can used a keypad to zoom in on one of the quadrants. Once zoomed in, the user can zoom out using the keypad as well. To clear, the user can either select a button on the keypad or the GUI. By implementing the design this way, we were able to incrementally increase complexity and allow for more complex interaction with the design. Also, the project allowed for manipulation and constant discovery of new designs and coloring with each set of selected parameters.
High-Level Design
The Julia Set is based off the equation 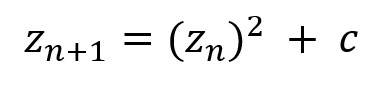 , where the z is a point on the complex plane z = x + iy, or for our purposes a pixel of interest on the TFT, and c is a complex constant. For each constant c, a new Julia Set can be generated. If the series converges for a given point, then the point is in the Julia Set and will be colored.
, where the z is a point on the complex plane z = x + iy, or for our purposes a pixel of interest on the TFT, and c is a complex constant. For each constant c, a new Julia Set can be generated. If the series converges for a given point, then the point is in the Julia Set and will be colored.
To accurately plot a Julia Set, we had to implement the computations in software and decided to also plot the Julia Set digitally. The TFT screen would provide enough resolution to visualize and comprehend Julia Sets.
Our design relates to the IEEE code of ethics through the nature of understanding and critiquing technical work.
Because the math associated with Julia Sets is public domain, there isn’t necessarily any patents/ copyrights/ or trademarks relevant to our project. Other existing online Julia Set generators may have their own copyright regulations, but these rights pertain to the rights over any images that are generated from their software.
Program/Hardware Design
Software Design
Buttons Thread:
This thread set the initial parameters from the Python GUI. Most notably, it designated the color that was selected from the Python GUI and set a designated color variable to 1 if the specified color was selected. In addition, it also set cref.real and cref.img values for the presets, and set value_selected = 1 to indicated that all information had been collected and pixels could now be calculated and drawn.
Slider Thread:
This thread was utilized to allow the used to manually input a complex number for c instead of using a preset. If the user changed the value of the real and imaginary sliders values and clicked the button, then the value selected for each slider was multiplied by 0.001 (to ensure the values were within the -1.5 and 1.5 for the real part and -1 to 1 for the imaginary part bounds). These values were then used later in the animation thread to calculate the divergence and color of the Julia Set for the given point.
Python Serial Thread:
Each time this serial thread runs it first sets the terminator character to ‘/r’ and sets the terminate count and time back to 0. The thread then spawns another thread to read the string from python sent over UART and put the string into a buffer. The first character of this buffer indicates what kind of event occurred, button, toggle, slider etc. For the slider, the thread scans the formatted buffer to get values for the slider id and the slider value and then sets the slider flag to 1 to indicate that there was a new event. For buttons, the flag is set to 1 to indicate that there was a new event and sets the button value based on if there is a press or release, 1 and 0 respectively.
Keypad Thread:
This thread was used to obtain a value from the keys on the keypad to determine whether the user wanted to zoom in on a quadrant or zoom out if they were already zoomed in. The keys on the keypad corresponded to the quadrants such that if one was selected, the TFT drew quadrant one of the Julia Set associated with the selected parameters. Two drew quadrant two, three drew quadrant three, and four drew quadrant four. Finally, if the user was already zoomed in on one of the quadrants, key 0 would redraw the full, zoomed out Julia Set.
Animation Thread:
The animation thread loop starts off by filling the entire TFT display with black and displaying the text “select a color” to indicate to the user to start the generation process. The thread is then yielded until the variable, color_selected, is set to 1, which happens when a color button press is acknowledged in the button thread. Next, in the animation thread, “select a preset or input value” is displayed and the thread is again yielded until the variable, value selected, is set to 1. This is set to 1 when a button press is acknowledged for a preset or for a sent slider value. The thread then initializes x_min, x_max, y_min, y_max, xstep, and ystep to display the entire image, in case there was a zoom in the last round. The x values are between -1.5 and 1.5 and the y values are between -1 and 1. The step value is set so there are 320 pixels in the x direction and 240 pixels in the y direction. Each point in the complex plane is hit in a nested loop structure, stepping through the x and y values. The initial z value, cp, is set to the point in the complex plane, with the real part being the x value and the imaginary part being the y value. In each round of the loop, doesNotConverge, is reinitialized back to 0. A loop then runs through the calculation z = z^2 + c, 90 times and if at any point in those 90 iternations the absolute value of the point passes 2, we count that as diverging and the loop breaks. If the absolute value does not pass that point after 90 iterations we record the final absolute value in the variable abs1 . The point in the complex plane is then mapped to the TFT display through the equations

If the point is not in the Julia Set, hence doesNotConverge equals 2, the pixel is drawn in white. If the point is in the Julia Set, the pixel is assigned a color based on its absolute value. The thread then yields for 10 seconds for the user to appreciate the image and then asks if they want to zoom in. If they press the corresponding quadrant button on the keypad the values of x_min, x_max, y_min, y_max, xstep, ystep, hfactor, and wfactor will change and the loop from before will run again with the new limits. The quadrant value is then set to 0 so a new zoom is not performed until the keypad is pressed. The user can zoom out by pressing 0 on the keypad reinitializing all the limits back to their original values. If cleared is pressed at any point and the system is not currently drawing the loop will end and set all of the color variable and quadrant values back to 0. The program then yields for 1 second and then begins again.
Main Function:
The main function initializes the TFT display and configures the threads. It then initializes a scheduler and schedules all of the above threads round-robin.
Python Software Interface Used In Design:
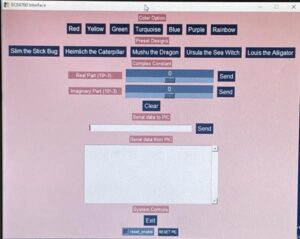
Hardware Design
The keypad was implemented as the main piece of hardware to allow for zooming in on a particular quadrant and zooming out to the full picture. On the keypad, buttons 1-4 were used to represent each of the four quadrants of the image (1 representing the top right quadrant, 2 as the top left, 3 as the bottom left, and four as the bottom right quadrant). Once zoomed in, button 0 was implemented to zoom back out to the full image.
The keypad was debounced through software to ensure that the program understood the inputs from the keypad correctly by ensuring that button bouncing did not interfere with the user experience.
This zoom functionality was implemented by redrawing only a single quadrant or redrawing the full image.
While creating this design, we found that image sophistication vs. time was our biggest obstacle. We could increase the complexity of our designs by increasing the number of iterations while determining convergence; however, this proved to significantly increase the drawing time. In the end, we opted for a 90 cycles compared to the initial 128 cycles because we could still achieve our desired complexity, but the drawing time was significantly reduced. Secondly, we wanted to implement further zooming using the quadrants (i.e. zoom into a specified quadrant and further zoom into the image produced). However, we found that the draw time for subsequent zooms was significant and the complexity was difficult to maintain. As a result, we opted for only zooming into one of the four quadrants on the initial image, and not account for zooming further than this.
Results of the Design
GIFs of Sample Julia Sets

Speed and Accuracy
The speed was measured by timing how long the program took to plot the selected Julia set. We found that the speed of the program heavily depends on the chosen value of the complex number C. For Julia sets in which most points diverge quickly, the plotter is significantly faster than when plotting sets with more convergence.
We measured the speed of two Julia sets as a performance metric:
Time to plot C = 0 + 0i (the black circle above): 60 seconds
Time to plot C = -0.8 + 0.156i (our “Ursula” preset): 42.44 seconds
The accuracy of the program was determined by comparison between our plotted Julia sets and online Julia Set generators (in particular, https://sciencedemos.org.uk/julia.php). Due to our number of iterations, limited resolution, and the fact that our plotter only plots points that converge and leave points at the edges white, we found expected some inaccuracies.
As shown by these comparisons, our Julia Set plots do not plot the points that show up as lighter colors (green, yellow, pink, light blue) when plotted by the online Julia Set plotter. These points diverge, so we assign them as white. This provided us with an interesting insight into the accuracy of our project, which was that Julia Sets that have very little convergence (as depicted below) will not show up on the TFT.

Interference and Usability
This project does not interfere with other people’s designs as it involves wired connections between the computer and the PIC-32, and does not have an audio or RF component.
This project is an exploratory tool to investigate how complex number math can be visually expressed. The colors of the display can be selected and implemented in a way to allow for maximum comprehension by all people, including those with varying types and levels of color blindness to ensure maximum accessibility. To do this, we had color options that the user can select to use for individual use. Also, the presets allow for designs to be drawn that have a large amount of variation, so varying divergence within the design are more discernible.
Conclusions
One of the most interesting results that appeared through the completion of this project was the appearance of structures within the Julia Sets when printed with the “Rainbow” color option. When comparing the Heimlich the Caterpillar preset printed in Rainbow (the first of the rainbow screenshots) to the online-generated version, you can see that our implementation allowed for the visualization of internal structures within the Julia Set. This was of particular interest to us, as our expectations were to mimic the online generator, and we did not expect such internal structure.
One consideration in improving the project would be the use of a larger display. While the TFT was able to achieve a high level of complexity within the drawings, a larger display with higher resolution would allow for more complexity within the Julia Sets and better visualization of the designs. Though our plotting speed is quite slow, the speed is limited by the complexity and the calculations completed to generate the Julia Set. If there was more available memory, we could have likely computed the Julia Sets faster.
When making decisions regarding the course of the project, we were consistent with the IEEE code of ethics. Because our project did not involve many physical safety concerns, we could ensure that we were upholding safety. Similarly, we made sure that we accepted any criticisms from one another or from instructors while working on our code. In terms of safety considerations, there aren’t any significant concerns. Due to the nature of the project, there are no motors or components that could pose a safety threat to the user. Our project did not concern any specific legal considerations, and all of the information we used to understand and generate Julia Sets was open-source.
Appendix A:
The group approves this report for inclusion on the course website. The group approves this video for inclusion on the course YouTube channel.
Appendix B: Commented Program Listing
C Code

Python GUI Code

Source: PIC-32 Julia Set Generator
