Introduction
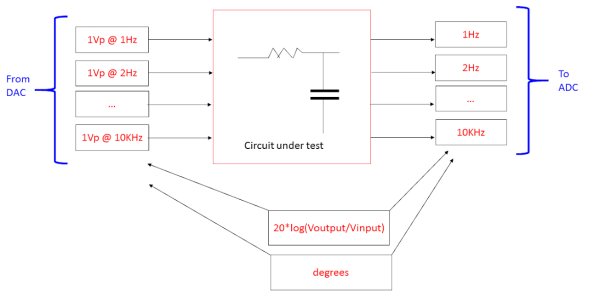
Frequency domain analysis is very important to know more about any system/ circuit or transfer function that we deal with. And the first thought comes to our mind about frequency domain analysis is “Bode plot“. Bode plot is a combination plot of magnitude and phase difference of output vs. input of a cosine wave of single frequency, when it is applied to a circuit.
Each of these cosine wave (signal) are applied once at a time and the frequency (in Hz or rad/sec) is increased in linear order (called chirp). All the while the amplitude of sine wave is kept constant (at say 1V_peak). While the frequency can be increased in small steps (1Hz/ sec), the time required to complete the entire frequency range can be quite big. Hence, it is preferred to choose 20 frequencies/ decade. For example, I had chosen 05Hz, 1Hz, 1.5Hz, 2Hz, 2.5Hz… 10Hz.
Generation (output) and sampling (input or feedback) of Sine wave
Generation of cosine wave (and sine) waveform is pretty straight forward, using floating point device and DAC. Be aware that using the sin or cos function from standard “math.h” library takes a lot of time (because, it is designed to meet a certain resolution, by iterative process). Instead, I am using a sine table (of 2048 points of amplitude, over 0 to 2*pi rad). I kept the “sampling” frequency (for both DAC and ADC) at 200KHz. Keeping a fixed frequency is vital to any digital signal processing algorithm.
Now the complication, if different output frequencies are needed: –
- Keeping sampling frequency of 200KHz and output of 1Hz = 200,000 points in 1 sine table.
- Keeping sampling frequency of 200KHz and output of 10KHz = 20 points in 1 sine table.
Obviously, a straight forward approach of a single sine table will not suffice. Hence, I use a linear interpolation technique. If the angle is such that direct output is available from the 2048 sine table, the the value is directly used. For values of angle in between, the amplitude is arrived using linear interpolation of 2 nearby values. For higher frequencies, the points in sine table are skipped (and interpolated). A function is written, which take care of all these logic and outputs the amplitude for any angle needed.
I could have used external DDS chips such as AD9833, but knowing both the sine and cosine of signal being generated, makes the magnitude and phase detection simpler (explained later). If I had used externally (DDS) generated signal, then I would have known the “frequency” of output signal (by knowing the SPI command of frequency that I send to AD9833), but knowing the phase is impossible, without sampling. And then, we would have needed separate means to get 90-deg phase shifted waveform.
Anti aliasing filter at DAC output
Using DAC is pretty simple. We just need to scale the float value from +1 to -1 (peak value of sine waveform) to 2048 (half of max value of 12-bit DAC, 4096). While using DAC makes life easier, there are some complications. Firstly, the DAC performance is decided by settling time. In case of STM32F407, the settling time is 3uSec, which translates to a max frequency of (1/3uS) = 333.33KHz . Hence, my choice of 200KHz sampling rate is safe (without introducing non-linearity in output cosine waveform.