The FFT (Fast Fourier Transform) first appeared when microprocessors entered commercial design in the 1970s. Today almost every oscilloscope from high-priced laboratory models to the lowest-priced hobby models offer FFT analysis. The FFT is a powerful tool, but using it effectively requires some study. I’ll show you how to set up and use the FFT effectively. We’ll skip the technical description of the FFT, because its already implemented in the instruments. Instead I’ll focus on the practical aspect of using this great tool.
The FFT is an algorithm that reduces the calculation time of the DFT (Discrete Fourier Transform), an analysis tool that lets you view acquired time domain (amplitude vs. time) data in the frequency domain (amplitude and phase vs. frequency). In essence, the FFT adds spectrum analysis to a digital oscilloscope.
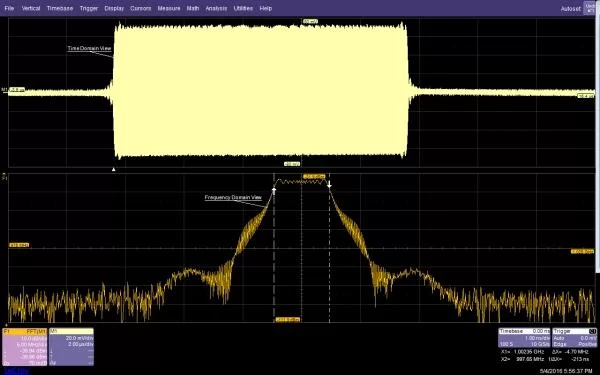
If you look at upper trace in Figure 1, you’ll see an amplitude-modulated carrier that uses a trapezoidal pulse as the modulation function. If you look at the time-domain view in Fig. 1 and I ask you to tell me the bandwidth of the signal, you’d have a hard time. But take the FFT of this signal and you get another point of view. The signal has a linearly swept frequency and the bandwidth, marked by the cursors, is 4.7 MHz. That’s how the FFT adds to the capability of the oscilloscope, it provides another point of view for the same data.
Figure 1. The time domain view in the top grid shows a pulse modulated RF carrier while the frequency domain view in the lower grid shows a uniform distribution of the carrier frequency between 997 MHz and 1002 MHz.
Read more: FFTs and oscilloscopes: A practical guide