Current Divider Circuits Explained with Formula and Practical Hardware

When designing an electronic circuit, there are lots of situations when a circuit requires different values of voltage and current sources. For example, when setting the preset voltage for an Op-Amp, it is very common to use a potential divider circuit to obtain the required voltage values. But what if we need a specific value of current? Similar to the voltage divider, there is another type of circuit called current divider which can be used to divide the total current into several within a closed circuit. So, in this tutorial, we will learn how to build a simple current divider circuit using the resistive method (using only resistors). Do note that it is also possible to make a current divider using inductors and the working of both the circuit will be the same.

Working of Current Divider Circuit

A resistor is the most used passive component in electronics and it is very easy to construct a current divider using resistors. The current divider is a linear circuit that split the total current flowing into a circuit and creates a division or produces a fraction of the total current.

According to the current divider rule, the current flowing through any parallel branch of a circuit will be equal to the product of total current and the ratio of opposite branch resistance to total resistance. Thus with the current divider rule, we can calculate the current flowing through a branch if we know the total current and resistance value of other branches. We will understand more about this as we proceed.

The current divider can be built easily using KCL (Kirchhoff’s Current Law) and Ohms Law. Let’s see how this division takes place into a parallel-connected resistive circuit.

In the above image, two resistors of 1 Ohm are connected in parallel, which is R1 and R2. These two resistors share the total current flowing through the resistor. Since the voltage across these two resistors is the same, the current flowing through each resistor can be calculated using the current divider formula

Thus the total current is I_Total = I_R1 + I_R2 as per Kirchoff’s current law.

Now to find the current of each resistor, we use Ohms law I = V/R on each resistor. In such a case,

IR1 = V / R1 and IR2 = V / R2

Therefore, if we use these values in I_Total = I_R1 + I_R2, the total current will be

Total Current = V / R1 + V / R2
= V (1 / R1 + 1 / R2)

Thus,

V = Itotal (1 / R1 + 1 / R2)-1
= Itotal (R1R2 / R1+R2)

So, if we can calculate the total resistance and the total current, then by using the above formula, we can get the divided current through the resistor. The current divider rule formulae to calculate for current through R1 can be given as

IR1 = V / R1
= Itotal [(1 / R1) / (1 / R1 + 1 / R2)]
IR1 = Itotal (R2 / (R1 + R2))

Similarly, the current divider rule formulae to calculate for current through R2 can be given as

IR2 = V / R2
= Itotal [(1 / R2) / (1 / R1 + 1 / R2)]
IR2 = Itotal (R1 / (R1 + R2))

Therefore, where the resistors are more than two, one needs to calculate the total or equivalent resistance to find out the divided current in each resistor by using the formula

I = V / R

Testing Current Divider Circuit in Hardware

Let’s see how this current divider works in a real scenario.

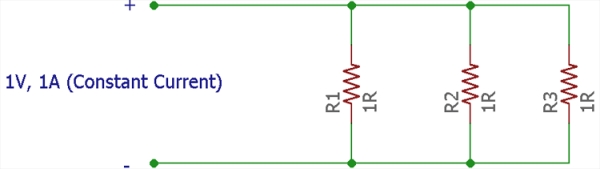
There are three resistors in the above schematic which are connected to a fixed or constant current source of 1A. All resistors are rated as 1 Ohm. Therefore R1 = R2 = R3 = 1 Ohm.

This circuit is tested in breadboard by connecting the resistors one by one in a parallel configuration with a 1A constant current source connected across the circuit. You can also check this simple constant current circuit to learn how current source works and how to build one on our own. In the below image, a single resistor is connected across the circuit.

The current is showing 1A in the multi-meter when connected across the resistor. Next, a second 1 Ohms resistor is added. The current dropped to half, approximately 500mA in each resistor as shown below

Why this has happened? Let’s find out using the current divider calculation. When two resistors of 1 Ohm are connected in parallel connection, the equivalent resistance will be –

REquivalent = (1 / (1 / R1 + 1 / R2))
= (1 / (1 / 1 + 1 / 1)
= 0.5 Ohms

Therefore, when two 1 Ohm resistance connected in parallel, the equivalent resistance became 0.5 Ohms. Thus, the current through the R1 is

IR1 = Itotal (Requivalent / R1)
IR1 = 1A (0.5 Ohms / 1 Ohms)
= 0.5 Amps

The same amount of current is flowing through the other resistor because R2 is the same 1 Ohms resistor and the current is constant up to 1A. The multimeter is showing approximately 0.5 Amps which is flowing through the two resistors.

Now an additional 1 Ohm resistor is connected in the circuit. The multimeter is now showing approximately 0.33A of current is flowing through each resistor.

Because there are three resistors connected in parallel, let’s find out the equivalent resistance of the three resistors in parallel connection

Requivalent = (1 / (1/R1 + 1/R2 + 1/R3))
Requivalent = (1 / (1/1 + 1/1 + 1/1))
Requivalent = 1 / 3
Requivalent = 0.33 Ohms

Now, The current through each resistor,

IR = Itotal (Requivalent / R1)
IR = 1 Amp x (0.33 Ohms / 1 Ohms)
IR = 0.33 Amp

The multimeter is showing approximately 0.33 Amp is flowing in each resistor as all the resistors are 1 Ohm in value and connected in a circuit where the current flow is fixed with 1A. You can also watch the video at the end of the page to check how the circuit works.

Current Divider Applications

The main application of the current divider is to produce a fraction of the total current available in the circuit. However, in some cases, the component that is used to carry the current has a limit of how much current actually flows through the component. Overcurrent causes increased heat dissipation, as well as reduces the life expectancy of the components. By using a current divider, the current flowing through a component can be minimized and thus smaller component size can be used.

For example, in a case where larger resistor wattage is required; adding multiple resistors in parallel decreases the heat dissipation, and smaller wattage resistors can do the same job.

Source: Current Divider Circuits Explained with Formula and Practical Hardware