Summary of DTMF Touch Tone Decoder Using Microchip PIC Microprocessor using PIC12F683
This project details a DTMF Touch Tone Decoder using the Microchip PIC12F683 microprocessor. It detects programmed sequences of DTMF tones via an audio input by using the Goertzel algorithm to process tone frequencies. The microprocessor is programmed with a hex file, and the output goes high upon detecting the target tone sequence, enabling control of external circuits. The system uses an ADC to sample audio signals shifted to fit the 0-5V input range. The design includes a 5V regulator and requires external components per the circuit schematic. The method allows robust tone detection even in noisy environments.
Parts used in the DTMF Touch Tone Decoder Using Microchip PIC Microprocessor:
- Microchip PIC12F683 Microprocessor
- 5V Regulator (such as LM7805)
- Audio input interface components (capacitors, resistors for signal shifting and conditioning)
- Power supply (regulated 5V source)
- Programming hardware for PIC microcontroller
- DTMF tone generator (telephone or equivalent device)
DTMF Touch Tone Decoder Using Microchip PIC Microprocessor
This project contains the details of using a Microchip PIC12F683 8 bit microprocessor to detect DTMF tones. The completed program allows the processor to be programmed with a string of DTMF tones to detect. If the programmed string is detected in the audio applied the audio input, the output will turn on (go high), and can be used to control other circuitry of the users design.
UPDATE! 11/2/2010:
Due to requests for the source code, I have attached it. I have created a new step (Step 9) containing the *.asm file, along with some important notes.
UPDATE! 10/12/2010:
The HEX file for progdramming that I originally attached to this instructable had a bug that prevented successful programing of the tone sequence, unless the microprocessor was in serial output mode while in programming mode. The HEX file attached now works properly. Sorry for any inconveniene caused for those who may have tried the original code.
I have included the *.hex file needed to program the microprocessor, 12F683_DTMF_DECODE_01A.HEX. You will need a programmer for PIC microprocessors. I have seen instructions on this site for building your own, but I cannot speak for any of them. The programmer I use came from a company called Micro Engineer Labs, Inc at www.melabs.com.
The only other parts needed are the electronic components, as shown in the schematic in step 3, Circuit Details. Digikey (www.digikey.com) is an excellent source for electronic components .
A telephone or other means of generating DTMF tones is also needed for programming the microprocessor with the the sequence of tones you want to detect. This is described in more detail in step 4.
Quick DTMF Overview
There are a total of 8 tones used to represent DTMF or “touch tone” numbers. The tones are in two groups of four, often referred to as the low and high tones. A number is represented by an audio waveform consisting of the sum of one of the low tones and one of the high tones. This can easily be visualized in a matrix format, as shown in the figure. Note that the DTMF system actually allows a total of 16 different tone pairs. The A, B, C, and D tones shown on the right hand column of the keypad in the figure are not included on a normal telephone, but they are often included on two way radios that have a DTMF keypad. They are sometimes used by two way radios for business or ham radio. The software for the project will also detect these additional 4 tone pairs.
Signal Processing Algorithm Description
The PIC 12F683 microprocessors built in A/D converter is used to sample an input audio waveform. The samples are analyzed using the Goertzel algorithm to detect whether any of the 8 tones are present.
The Goertzel algorithm is a signal processing algorithm which is used for detecting a single frequency. It acts as a very narrow bandpass filter. It produces a very sharp response to frequencies within the pass band, and a much lower response for frequencies outside the pass band.
In my implementation of the algorithm, the samples are taken at a rate of 4 times the frequency to be detected. Using a sample rate of 4 times the target frequency makes coefficients used in the algorithm be equal to 1 or 0. This eliminates the need to perform complicated and time consuming multiplication on an 8 bit micro. I haven’t included all the mathematical details of the algorithm here, but a Google search will produce articles on the topic if you are interested in learning more about the algorithm itself.
Due to the restriction that the sampling rate must be 4 times the target frequency, the sample rate required will be different for each of the 8 tones that are used for DTMF. So, the algorithm must be run once for each of the 8 frequencies . This means that a separate set of samples must be taken for each frequency of interest, as each frequency will be tested at a different sample rate.
The sharpness of the filter response versus frequency is proportional to the number of samples taken. The response of the algorithm must be sharp enough that it responds to the target frequency, but does not respond to any of the other 7 frequencies. A value of 120 samples was found to produce a reasonably narrow response in experimentation. There is of course a tradeoff between number of samples and the execution time. In order to detect short tones, the execution time should be as short as possible. But, to make a narrow response the number of samples must be larger, resulting in a longer execution time. The number of samples becomes the limiting factor in how short of a tone can be detected.
Once the algorithm has processed 120 samples, it outputs a value. The magnitude of this value is proportional to the amplitude of the frequency of interest. This resulting value is compared against a threshold to determine if target frequency is present.
Once the algorithm has been run for all 8 frequencies, the microprocessor performs logic on the results to determine if a valid DTMF pair is present. A valid DTMF pair is considered to be present only if 1 row freq and 1 col freq is detected. Other combinations are regarded as invalid.
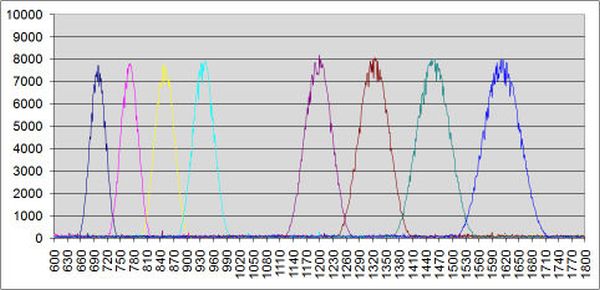
The graph shows the actual response measured using this algorithm running on a PIC 12F683. The graph shows the frequency response of all 8 times the algorithm is run. The x axis is frequency, in Hz. The vertical axis is the value output by the algorithm. The input was a 1V sine wave, swept from 600Hz to 1800Hz. Note that the width of the response is wider for the higher frequency filters. This is due to the fact that the width of the response is proportional to the sample rate, divided by the number of samples taken. In this implementation of the algorithm, the sample rate is always four times the target frequency, to simply and speed up the math. However, the same number of samples is used for each of the 8 target frequencies. The to make the width of the response the same for each would require using the same sample frequency for each, which would involve more time consuming mathematics, or it would require that the number of samples taken at the higher frequencies be greater, which would lengthen the execution time. If you were using a microprocessor with real DSP functionality, the extra math could be performed very fast and so it would be something that you would most likely include.
Despite the differences in the width of the response, the operation has been very robust at detecting tones, even in the presence of significant noise.
Circuit Details
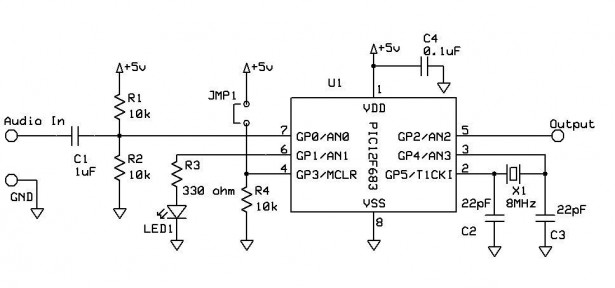
The A/D converter measures voltages between 0V and 5V. The audio input will be a signal that swings above and below 0 volts, so its waveform will have positive and negative portions. In order to sample the input audio waveform with the A/D converter, the input signal needs to be shifted.